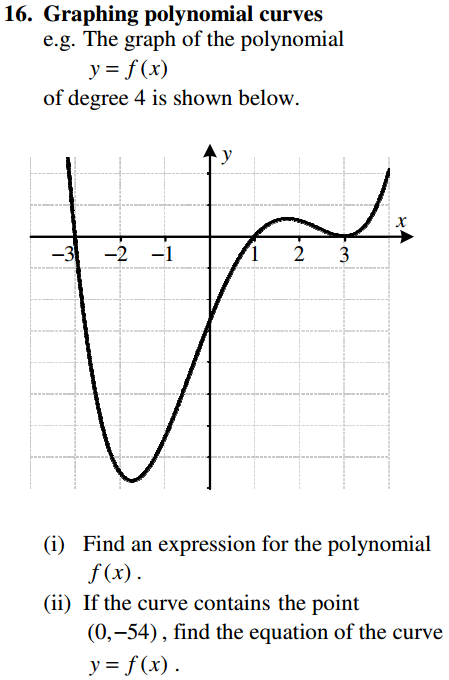
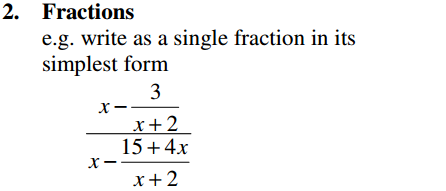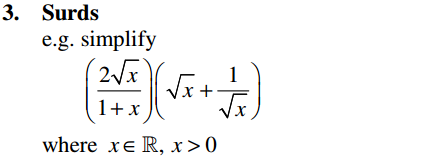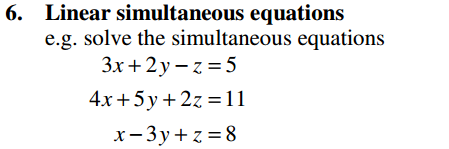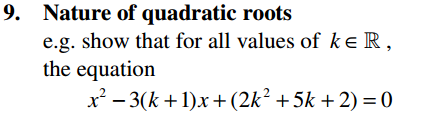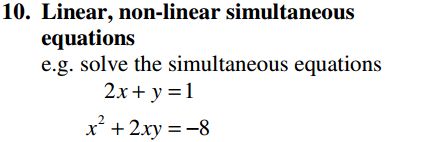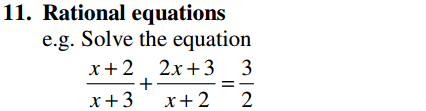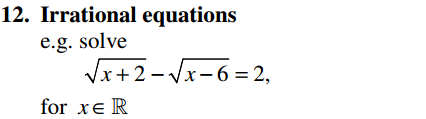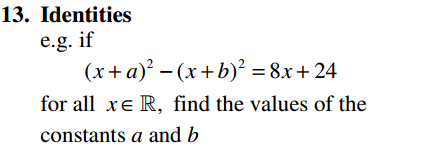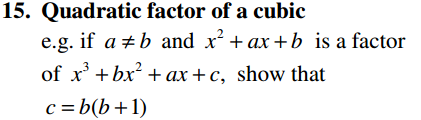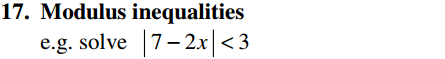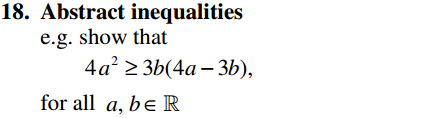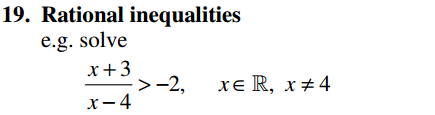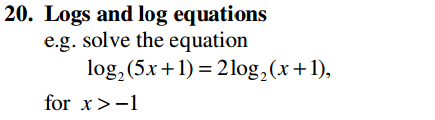Algebra Overview

---

Revision Notes

Algebra Exam Questions

---

For a reasonably comprehensive revision of Algebra this page contains 3 Printable Worksheets with solutions.

Algebra Revision Worksheet Questions

Algebra Revision Worksheet Solutions

---

22 Revision Questions

22 Algebra Revision Questions

Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7 i

Solution 7 ii

Solution 7 iii

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Solution  20

Solution  21

Solution  22

---

4 Revision Questions

Induction Revision Questions

4.  Prove de Moivre's Theorem using induction

Solution 1

Solution 2

Solution 3

Solution 4