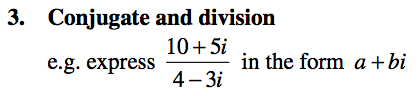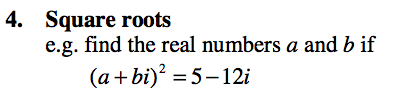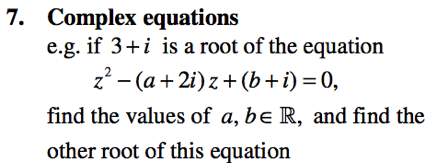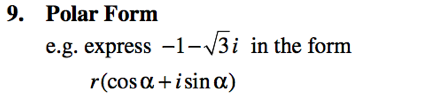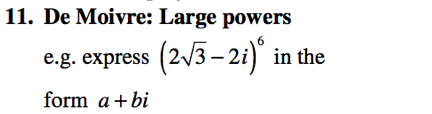Complex Numbers

---

1. Irrational numbers

Irrational numbers​ - surds

Construct root 2

Using a compass and straight edge

Construct root 3

Using a compass and straight edge

---

2. Complex numbers introduction

Equation with imaginary roots

Quadratic equation with imaginary roots

Using the quadratic formula

Addition and multiplication of complex numbers 

---

3. Division and equity of complex numbers

Dividing by a complex number - conjugate

Expressing a fraction with a real denominator

Complex number equations

"Real = real, imaginary = imaginary"

---

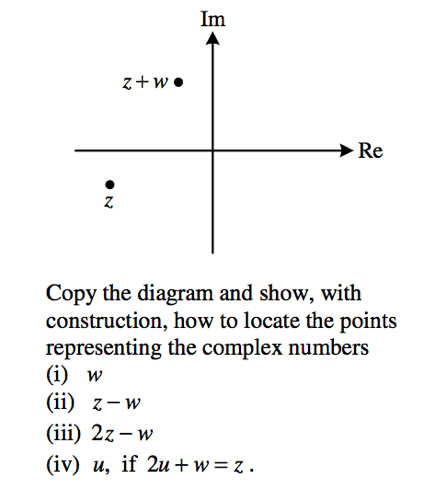
4. Argand diagram - modulus

Plot on an Argand diagram
Calculate modulus

---

5. Transformations of complex numbers

Understanding multiplication

Multiplication involves scaling and rotating
​Addition involves shifting

Transformations involving multiplication

---

​6. Conjugate roots theorem

Quadratic equation - conjugate roots

Showing that a conjugate is a root

Solving a cubic equation with two imaginary roots

---

7. Polar form of a complex number

Converting from polar to rectangular form

Express in polar form

Finding the modulus and argument

---

8. Products and quotients in polar form

Multiplying and dividing in polar form

Multiplication: Multiply the module and add the arguments

Division: Divide the module and subtract the arguments

---

9. De Moivre's Theorem

Raising a number to a power - expanding

Express in polar form and expand

---

10. Applications of de Moivre's Theorem

Raising a number to a power

Proving trigonometric identities using de Moivre's Theorem

Finding roots

---

---

12 Revision Questions

Complex Number Revision Questions

1. Solution

2. Solution

3. Solution

4. Solution

5. Solution

6. Solution

7. Solution

8. Solution

9. Solution

10. Solution

11. Solution

12. Solution

---

---

Revision Notes

---

Complex Number Video

Powers of i

KA Powers of i

KA Complex Numbers and i

Introduction to Complex Numbers: Addition, subtraction, multiplication, powers of i.

KA Adding & Subtracting Complex Numbers

KA Multiplying Complex Numbers

Complex division in rectangular form

KA Dividing Complex Numbers

Solving Complex Equations:
 
Real parts = Real parts
Imaginary parts = Imaginary parts

Graphing complex numbers on an Argand diagram and finding the modulus of a complex number.

KA Argand Diagram (Complex Plane)

KA Modulus (Absolute Value) of a Complex Number

Transformations in the Complex Plane

Complex conjugate roots
Solving quadratic and cubic equations with imaginary roots.

Writing a complex number in Polar Form

Multiplying and dividing in Polar Form and using deMoivre's Theorem to expand a complex number to a power.

---

Using deMoivre's Theorem to find roots of a Complex Equation. 

Using deMoivre's Theorem to prove Trigonometric identities. This question also requires use of the Binomial Theorem.

---

The Syllabus

3.1 Ordinary & Higher Levels

4.1 Higher Levels